Mechanical instability and morphogenesis of fiber bundles under torsion
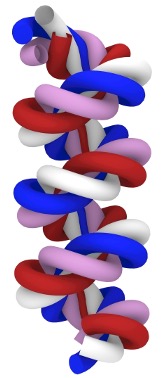
Helical structures are recognized as one of the characteristic geometric forms found in a wide range of structures, from microstructures like DNA and proteins to macrostructures such as twisted yarn and steel wire cables. Although most artificial helical structures are created through the torsional deformation of elastic filaments, the mechanical instability of the structure, which occurs at a critical torsion angle, and the subsequent development to plectoneme and other geometrical structures are not well understood. We are investigating the geometry and nonlinear mechanics of helical structures under torsional deformations by combining experiments and MPM simulations.
Geometrical design of Amigami, Kirigami, Origami, and Metamaterials

It is well-known that thin structures, like paper, are more susceptible to out-of-plane bending deformation compared to in-plane stretching due to their inherent geometrical properties. Traditional Japanese arts such as origami and kirigami take advantage of this inherent flexibility of two-dimensional materials. In our research group, we are exploring a novel approach called “amigami” to design curved surfaces by harnessing the flexibility of paper sheets. Additionally, we are investigating the development of mechanical metamaterials on curved surfaces through the application of geometric structural design principles.
Fracture, friction, and contact mechanics and physics of elastomers

Elastomers, including gels and rubbers, exhibit highly flexible deformation properties, primarily attributed to entropic elasticity arising from the molecular chains’ cross-linked structures. In our research group, we focus on modeling and numerical analysis to understand the nonlinear mechanics of elastomers, encompassing fracture, friction, and contact mechanics. Our approach integrates principles from applied mathematics and physics. Particular attention is devoted to the quantitative comparison between theoretical and numerical analyses and experimental results.
Differential geometry as a new mathematical basis for defects in crystal

Dislocations and disclinations are common lattice defects, known as line defects, in crystalline materials. Dislocations have been extensively studied both theoretically and experimentally, while disclinations have received comparatively less attention, and their kinematics remain poorly understood. In our research group, we aim to model disclinations using continuum mechanics on Riemannian-Cartan manifolds. This geometric analysis significantly expands the framework of conventional lattice defect theory.
Materials Transactions (2023, in press)
Exploring sustainable structural design through plant morphodynamics

Today, global awareness of environmental sustainability is growing at an unprecedented rate. To preserve the current environment for future generations, we must depart from conventional practices of mass production and consumption in manufacturing and instead develop new, highly sustainable structural design principles. Throughout their extensive history, countless plant species have faced elimination, with only those capable of surviving intense competition evolving into their present-day forms. By emulating these remarkable plant structures, it is believed that we can establish unconventional and sustainable guidelines for structural design. In our research group, we are presently studying plant dynamics through the lens of Riemannian manifolds.
Simulation-based machine learning system for efficient control of soft robots

Soft robots, consisting of a continuum of infinitely deformable degrees of freedom, are anticipated to exhibit flexible locomotion resembling that of humans and animals, in contrast to conventional rigid robots with a limited number of degrees of freedom. Nevertheless, controlling the motion of flexible structures is challenging, necessitating the development of novel control principles based on nonlinear dynamics. Our research group is undertaking the task of constructing a new control system by integrating nonlinear dynamics simulation and machine learning, and we are actively engaged in research to demonstrate its feasibility.
